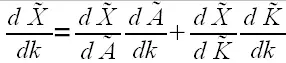Hier die Herleitung etwas ausführliche als im Script, es finden zwei Ableitungsregeln Anwendung - wusste sie aus dem Matheunterricht nicht mehr und habe sie hier aufgefrischt
Auf einen Blick: Ableitungsregeln und Ableitungen
Produktregel in Zeile 4&5 unten
Kettenregel in Zeile 6 unten
[TEX]\begin{eqnarray*}
X & = & k\widetilde{X}\left(\frac{\overline{A}}{k},\frac{\overline{K}}{k}\right)\\
u & = & k\\
v & = & \widetilde{X}\left(\frac{\overline{A}}{k},\frac{\overline{K}}{k}\right)\\
\frac{dX}{dk} & = & \frac{du}{dk}\cdot v+\frac{dv}{dk}\cdot u\\
& = & 1\cdot\widetilde{X}\left(\frac{\overline{A}}{k},\frac{\overline{K}}{k}\right) + \frac{d\widetilde{X}}{dk}\cdot k\\
\frac{d\widetilde{X}}{dk} & = & \frac{d\widetilde{X}}{d\widetilde{A}}\frac{d\widetilde{A}}{dk}+\frac{d\widetilde{X}}{d\widetilde{K}}\frac{d\widetilde{K}}{dk}\\
\frac{d\widetilde{A}}{dk} & = & -1\cdot\frac{\overline{A}}{k^2}\\
\frac{d\widetilde{K}}{dk} & = & -1\cdot\frac{\overline{K}}{k^2}\\
\frac{d\widetilde{X}}{dk} & = & -\frac{d\widetilde{X}}{d\widetilde{A}}\frac{\overline{A}}{k^2}-\frac{d\widetilde{X}}{d\widetilde{K}}\frac{\overline{K}}{k^2}\\
\frac{dX}{dk} & = & 1\cdot\widetilde{X}\left(\frac{\overline{A}}{k},\frac{\overline{K}}{k}\right)+(-\frac{d\widetilde{X}}{d\widetilde{A}}\frac{\overline{A}}{k^2}-\frac{d\widetilde{X}}{d\widetilde{K}}\frac{\overline{K}}{k^2})\cdot k
\end{eqnarray*}[/TEX]
Ab der letzten Formel nur noch das k kürzen und du hast das Ergebnis im Script.
Hilft das weiter?