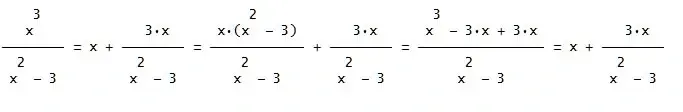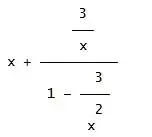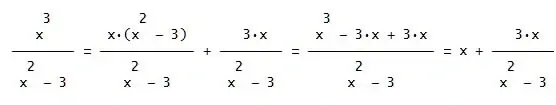Kurvendiskussion S. 32

Ich habe mir nun mehrmals die Termumformung auf S. 32 unter dem Punkt iv) angesehen und auch erst geglaubt dass sie korrekt ist, nachdem ich für x werte eingesetzt haben. unglaublich was man alles wie umformen kann.

Mir ist absolut nicht klar wozu diese Umformung nötig ist, auf welchen gesetzmässigkeiten sie beruht und was mit der bloßen umformung nun deutlicher zu erkennen sein soll als vorher???????????????😕

Was ist den das Ziel?
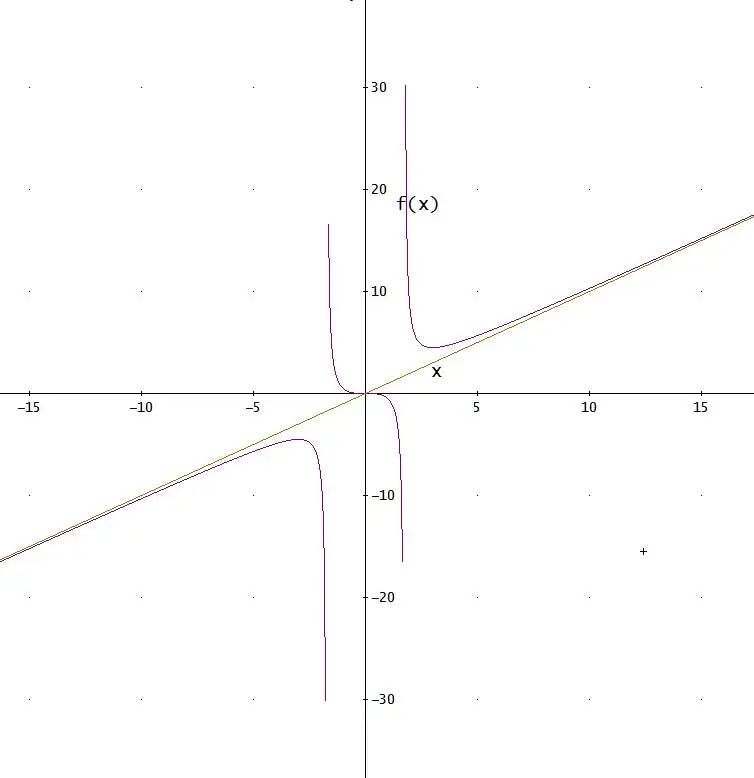
Untersuchung der Funktionswerte an den äußeren Rändern!
Ist das Ziel durch eine Umformung eine eventuelle Begrenzung zu erkenne, das x also nicht gegen unendlich gehen kann, oder wozu wurde das hier so gemacht.
und wenn ja - auf solch umformungen komme ich nie im leben:eek

Die haben einfach eine Polynomdivison durchgeführt.

Schau mal hier, dadurch habe ich es dann (nach anfänglichen Schwierigkeiten) auch nachvollziehen können:

Verhalten im Unendlichen - Rationale Funktionen

Vielen dank. Genau das gleiche Onlineskript arbeite ich inzwischen auch durch. Dort wird alle einfach erklärt. Hilft mir sehr.
Ich habe den Kurvendiskussion noch parallel dazu in ein Matheforum gepostet und folgende Antwort dadurch erhalten:

Der letzte Term auf S. 32 stellt x allein vor den Bruch und da bei dem letzten Bruch immer ein Nullwert (0, oder 0,...) rauskommt, steht das x quasi allein da. Wenn x nun gegen unendlich geht, bewegt sich folglich auch der komplette Term gegen unendlich.

Danke für die Antwort.

eee!! Ich kapier das immer noch nicht. Könntet ihr evtl. den Rechenweg posten? Das wäre super.
VG Caro

wenn man den bruch mit x^2 im nenner und zähler dividiert erhält man



diese umformung hilft insofern, als dass man erkennt dass sich der term für x -> und x -> - gegen null bewegt. man muss dazu nur den zähler betrachten, der für größer werdende x immer näher zu null hin geht und somit nähert sich der ganze term mit größer werdenden x null.

der graph nähert sich also mit größer werdenden x immer mehr f(x)=x (=asymptote)

damit es noch besser verständlich ist, hier der graph: