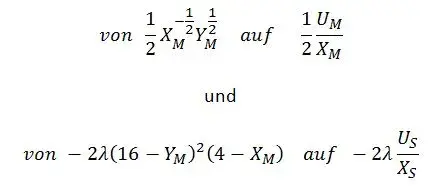Edgeworthbox und Lagrange in Übungsaufgabe 4

Mitstreiter,

ich stehe ein wenig auf dem Schlauch bei der Lösung der Übrungsaufgabe 4 von Seite 18 der KE 3:

Nach Aufstellung der Gleichung habe ich im zweiten Teil ... + lambda [16 - ((4-Xm)(16-Ym))^2]

Diesen Term würde ich nun nach der Kettenregel nach dXm ableiten. Also äußere Ableitung * innere Ableitung,

- 2 lambda (4-Xm)(16-Ym) * - 1

Woher kommt nun das Quadrat im Ergebnis?:

+ 2 lambda (4-Xm)(16-Ym)^2

Vielen Dank für Eure Hilfe!

Die Ableitung ist:
[tex] \frac{d}{dX_M}(\lambda (16-(4-X_M)^2 (16-Y_M)^2) )=-\frac{d}{dX_M}(\lambda (4-X_M)^2 (16-Y_M)^2 )=[/tex]
[tex] =-\lambda (16-Y_M)^2 \frac{d}{dX_M}(4-X_M)^2=-\lambda (16-Y_M)^2 2(4-X_M) \frac{d}{dX_M}(4-X_M)=[/tex]
[tex]=2\lambda (16-Y_M)^2 (4-X_M).[/tex]

Jetzt hab ich's -

Ich schließe mich der Frage an:

Wie kommt man in Schritt (4) anschließend

?

Steh gerade völlig auf dem Schlauch woher ich diese Interpretation nehmen soll.

Bei dem ersten Teil kann ich eine "Hilfsvariable" X^(0,5) / X^(-0,5) erahnen, hab aber keine Ahnung wie ich darauf kommen soll, wenn ich das Ergebnis nicht vorher sehe...

Bitte um Hilfe.

Ich kann nur antworten, WARUM sind diese Übergänge richtig. Aber die Frage, WOHER
soll man wissen, dass genau diese Übergänge notwendig sind, ist viel mehr schwer 🙁((

[tex] U_M=(X_M Y_M)^{1/2},\;\; \frac{U_M}{X_M}=\frac{X_M^{1/2} Y_M^{1/2}}{X_M}=X_M^{-1/2}Y_M^{1/2}[/tex]

[tex]U_S=X_S^2 Y_S^2=(4-X_M)^2 (16-Y_M)^2;\;\; \frac{U_S}{X_S}=(16-Y_M)^2 (4-X_M)[/tex]

Ich stehe bei dieser Aufgabe auch auf dem Schlauch bei der Überleitung in der Formel (9):
Ys*(Xm/Xs+1)=16 ->OK
Dann würde ich rechnen:
Ys = 16*Xs/Xm + 16/1 -> erweitern 16 mit *Xm/Xm
Ys = 16*Xs/Xm + 16*Xm/Xm = (16*(Xs+Xm))/Xm = 16*4/Xm

Wie kommt man zu Ys = 16/4*Xs?

Danke für Eure Hilfe!
Igor