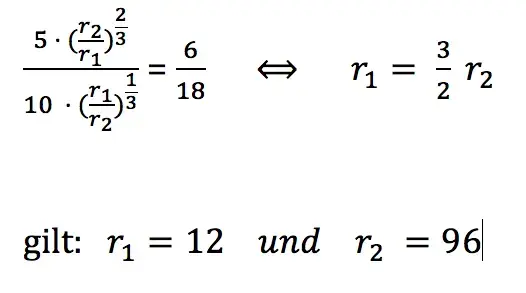Ableitungen Hilfe benötigt...

Habe folgende Aufgabe und verstehe einfach nicht, wie man auf das Ergebnis kommt. Ich leite offenbar falsch ab, wobei das eigentlich nicht so schwer sein sollte. Aber vielleicht kann mir ja mal jemand Schritt für Schritt erklären, wie man zu dem Ergebnis kommt.

Funktion im Anhang !

DANKE !

Hm.... glaube, dass da ein Tippfehler in Deiner Produktionsfunktion ist, weil [tex] r_1[/tex] fehlt. Ich unterstelle jetzt einfach mal, dass das erste [tex] r_2 [/tex] ein [tex] r_1[/tex] ist und Deine Funktion so aussieht: [tex] x = 15 * r_{1}^{\frac{1}{3}} * r_2^{\frac{2}{3}}[/tex]. Dann sehen Deine partiellen Ableitungen wie folgt aus

[tex] \frac{\partial x}{\partial r_1} = 15 * \frac{1}{3} * r_{1}^{-\frac{2}{3}} * r_2^{\frac{2}{3}} = 5*r_{1}^{-\frac{2}{3} }* r_2^{\frac{2}{3}[/tex]

[tex] \frac{\partial x}{\partial r_2} = 15 * \frac{2}{3} * r_{1}^{\frac{1}{3}} * r_2^{-\frac{1}{3}} = 10*r_{1}^{\frac{1}{3}} * r_2^{-\frac{1}{3}[/tex]

Jetzt den Quotienten bilden:

[tex] \frac{\frac{\partial x}{\partial r_1}}{\frac{\partial x}{\partial r_2}} = \frac{5*r_{1}^{-\frac{2}{3} }* r_2^{\frac{2}{3}}}{10*r_{1}^{\frac{1}{3}} * r_2^{-\frac{1}{3}}} = 0.5 * \frac{r_2}{r_1}[/tex]

ich kann Dir raten, evtl Klausurvorbereitung bei Fernstudium Guide mitzumachen, es sind noch Plätze frei. Der Dozent erklärt sehr gut und frischt alle Grundlagen auf, die Du brauchst. Ich hatte viele Probleme was Mathe angeht, jetzt aber nach dem ich die Vorlesung besucht habe, besser verstanden.

Vielen Dank für die Hilfe. Hattest Recht, habe mich am Anfang verschrieben. Die Ableitung habe ich nun auch hinbekommen, war ja wirklich nicht schwer. Jedoch irritiert mich, was in meiner vorgegebenen Lösung herauskommt.

Im Anhang die Lösung:

Dann ist ja ganz einfach, die negative Potenz bedeutet, daß die jeweiligen Unbekannten unter den Bruch gehören. Und da dann beide die gleiche Potenz haben, kann man diese ausklammern. Dann kann man den Ausdruck umdrehen, da teilen durch einen Bruch gleich Multiplikation mit dem Kehrwert bedeutet, dadurch fällt die Potenz auch weg, da 2/3 + 1/3 gleich 1 ist. Es bleiben 1/2 r2/r1 = 1/3. Dann nach r1 umstellen, müßte dann passen. Habe nicht genau nachgerechnet, habe gerade kein Papier zur Hand und mag nicht aufstehen