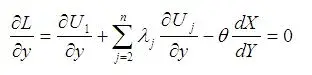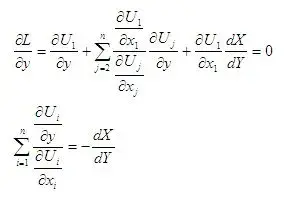00692 Theorie der Kollektivgüter I KE 1 Theorie der öffentlichen Konsumgüter
Hallo,
kann mir vielleicht jemand folgende Ableitung erklären? Auf Seite 5 der o.g. KE findet sich folgende Lagrange-Funktion:
[tex]
L:=U_1(x_1,y) + \sum_{j=2}^n \lambda_j[U_j(x_j,y)-\overline {U}_j]+\theta[\sum_{i=1}^n x_i-X(y)]
[/tex]
folgende Ableitung nach [tex]x_j[/tex] ist zudem angegeben:
[tex]
\frac{\partial L}{\partial {x_j}} = \lambda_j \frac {\partial U_j}{\partial x_j} + \theta = 0
[/tex]
warum steht am Ende das theta? in der Nebenbedingung gibt es doch gar kein xj und somit müsste der gesamte Summand als Konstante wegfallen oder?
Hallo,
kann mir vielleicht jemand folgende Ableitung erklären? Auf Seite 5 der o.g. KE findet sich folgende Lagrange-Funktion:
[tex]
L:=U_1(x_1,y) + \sum_{j=2}^n \lambda_j[U_j(x_j,y)-\overline {U}_j]+\theta[\sum_{i=1}^n x_i-X(y)]
[/tex]
folgende Ableitung nach [tex]x_j[/tex] ist zudem angegeben:
[tex]
\frac{\partial L}{\partial {x_j}} = \lambda_j \frac {\partial U_j}{\partial x_j} + \theta = 0
[/tex]
warum steht am Ende das theta? in der Nebenbedingung gibt es doch gar kein xj und somit müsste der gesamte Summand als Konstante wegfallen oder?